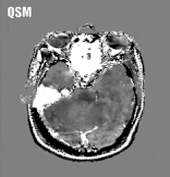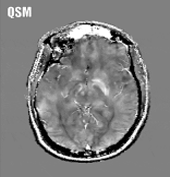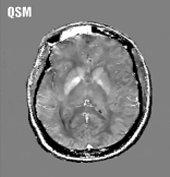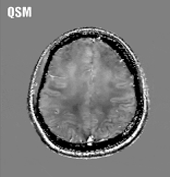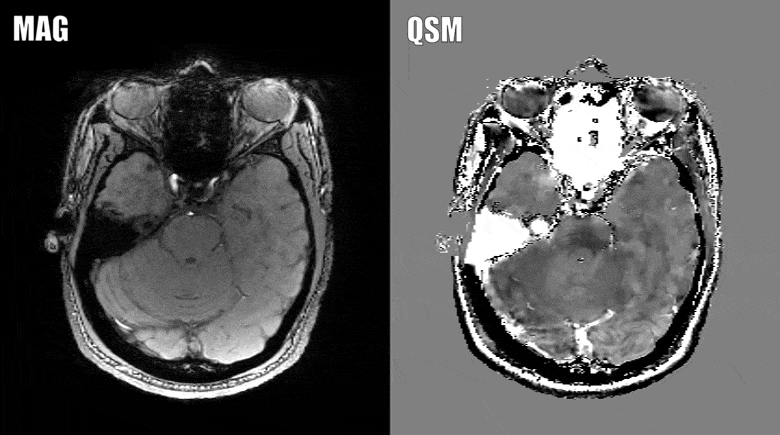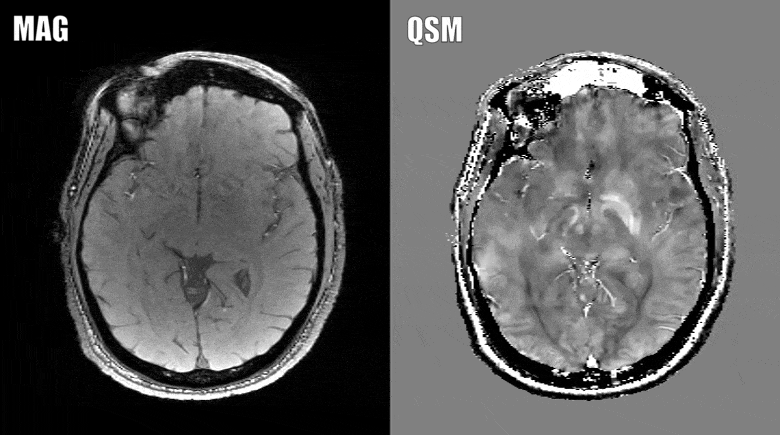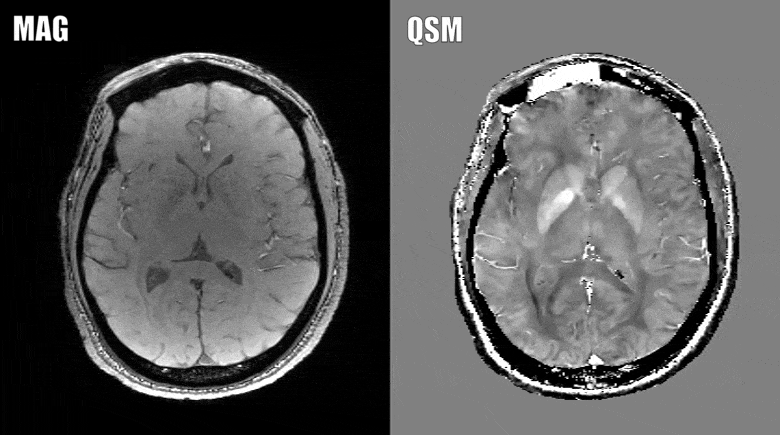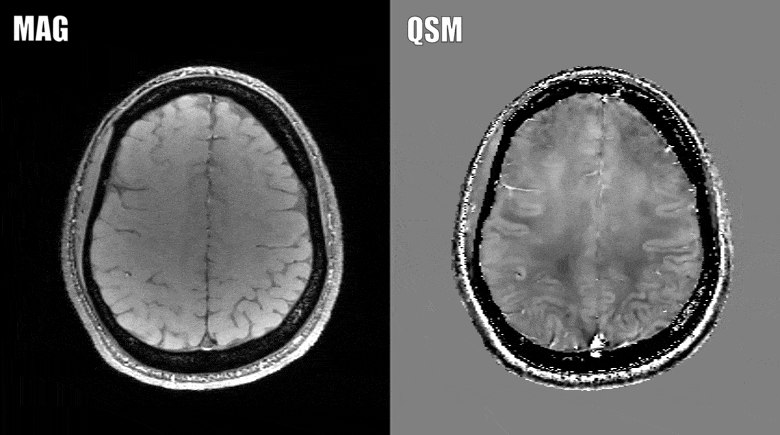
Quantitative susceptibility mapping (QSM) is a noninvasive magnetic resonance imaging (MRI) method that enables quantitative investigation of the tissue magnetic susceptibility, which has been applied to a wide range of biomedical problems. Algorithmically, QSM solves the magnetic field-to-magnetization (tissue susceptibility) inverse problem under conditions of noisy and incomplete field data acquired using MRI. Therefore, sophisticated numerical optimization methods are necessary to treat the ill-posed nature of the problem and their mathematical rationale and computational implementations are reviewed in this paper. The forward problem is typically presented as an integral form, where the field is given as the convolution of the dipole kernel and tissue susceptibility distribution. This integral form can be equivalently written as a wave-type partial differential equation (PDE). When noise and model errors are present, the PDE fundamental solution characterizes them as streaking and shadow artifacts in QSM reconstruction. These artifacts can be reduced using biomedical prior knowledge and the Bayesian maximum a posteriori estimation, which is known as morphological enabled dipole inversion (MEDI). The cost functions in Bayesian QSM are typically convex, allowing robust computation using gradient-based optimization methods such as quasi-Newton, split-Bregman, and primal-dual algorithms. Moreover, using prior knowledge based preconditioners (preconditioned MEDI) and additional regularizations imposing zero susceptibility on a homogeneous tissue, Bayesian QSM reconstruction can be accelerated, and shadow artifacts can be effectively reduced. Improving QSM speed is under active development, and a rigorous analysis of preconditioning needs to be carried out for further investigation.